Пойдет такая доска, или что не так?
Сморя зачем. Так-то не постирать, ни погладить, ни в шахматы сыграть. Фотки "Их разыскивает милиция" разве раазвесить? Доктора подождем, пусть он скажет...




Амальгама |
Привет, Гость! Войдите или зарегистрируйтесь.
Вы здесь » Амальгама » Лукоморье 2.0 » Доска Гальтона и связанный с нею парадокс
Пойдет такая доска, или что не так?
Сморя зачем. Так-то не постирать, ни погладить, ни в шахматы сыграть. Фотки "Их разыскивает милиция" разве раазвесить? Доктора подождем, пусть он скажет...
Сморя зачем.
А я откуда знаю, зачем?
Ты же просил:
Выпилил бы лобзиком доску да и фоткал бы процесс...
Я выпилил виртуальным лобзиком системы Paint, щас буду фоткать процесс,
а зачем оно тебе, я не знаю...
Мне нагляднее в виде буквенных строк, еще лучше в виде двоичных чисел.
Для себя я так и делаю, получается быстро и компактно.
А картинки, это исключительно для тебя:
Светлейший князь любил смотреть картинки
И посыпать лакеев конфетти
Он обожал с арбузов серединки
И выпил весь ликёр с коробки «Ассорти»
(с) Веня Д'ркин "Светлейший князь"
Отредактировано Лукомор (2023-06-05 07:45:11)
Если же зачем тема целиком
Да, я это имел в виду. Но потом вдруг:
то я ей занимался пару лет, пока для себя все прояснил.
А вопрос то был Зачем ? Ну в том смысле какая цель всей темы ? Или какая задача ? Зачем этим всем заниматься, если и так все вроде понятно ...
Зачем этим всем заниматься, если и так все вроде понятно ...
Чтобы другим тоже понятно было. Исследователь всегда хочет поделится своими мыслями и опытом.
А вопрос то был Зачем ?
Ответа на данный вопрос, который бы начинался со слов:"Для того, чтобы (что?)...",-
не существует.
Есть ответ, который начинается со слов:"Потому что гладиолус!...". 
Потому что меня всегда, сколько себя сознаю, интересовали вопросы детерминированного
и случайного, и насколько детерминированное случайно, а случайное - детерминировано.
Даже не так. Меня с детства интересовали всякие занимательные задачки из разных
научно-популярных журнальчиков и детских книжек.
Про вероятностную доску Гальтона я прочитал в какой-то из таких популярных книжек, и
тут же почти забыл. Лет семь назад подобная тема - про шашку на шахматной доске
внезапно всплыла на одном научном форуме, и занимала меня пару лет, что выразилось
в интенсивной (более 400 сообщений, на форуме, в личных сообщениях и электронной
почтой) переписке.
Там же лроскользнула и картинка детерминированной доски Гальтона, которую доску
я сейчас и выпилил фотолобзиком для Шарпера.
И она благополучно проскользнула тогда мимо моего сознания, которое было поглощено
ыероятностной шахматной доской. И вот теперь, снова переживая ту старую тему,
я опять вспомнил про эту детерминированную доску, и решил подарить ее Шарперу.
Но посмотрев внимательно на фото, я сначала придумал занимательную
задачку:
" восстановить по рисунку начальное положение всех переключателей и номера всех
шариков в карманах, в порядке очередности их движения по доске.".
Эта задачка легко решается, поскольку она вычислительно приводимая,
однако для данной конфигурации шариков решения не имеет, поскольку
на фото приведено невозможное состояние процесса, которое не может быть получено ни
при каком начальном положении переключателей. Решение оказалось простым и забавным,
и я решил им поделиться, пока опять не забыл.
Потом я вдруг понял, что детерминированную доску Гальтона до сих пор вообще
никто не изучал, и кроме одной маленькой популярной статьи в интернете, с единственной
( с двумя вообще-то!) фотографией, и рассмотрел уже общий случай для небольшого
количества уровней, со всеми возможными начальными состояниями переключателей,
которых для доски с одним уровнем всего 2, для доски с двумя уровнями уже 8,
для доски с тремя уровнями - 64, с четыремя уровнями = 1024, с пятью уровнями =3 2768,
и наконец, с шестью уровнями 2 097 152. В общем же случае, для доски Гальтона
с n уровнями, переключателей для треугольной доски будет: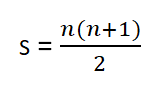
(энное треугольное число, что для треугольной доски вполне естественно),
а количество различных одновременных состояний этих переключателей будет равно: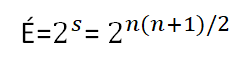
При этом, если начать с любого начального состояния переключателей, то
после 2^n различных маршрутов состояние переключателей возвращается в
исходное, и в этом цикле из É возможных состояний переключателей
реализуется только :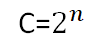
Из этого следует, что все возможные начальные положения переключателей разбиты на: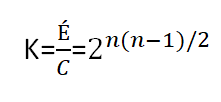
различных циклов, и никакой переход из одного цикла в другой невозможен.
Можно только начать с любой комбинации из принадлежащих данному циклу,
это будет начальная фаза процесса, но перейти из одного цикла в другой,
когда процесс запущен, уже нельзя.
Потом я нашел простое правило, по которому можно определить принадлежность
конкретного состояния переключателей тому или иному циклу.
Впрочем, я увлекся и отвлекся от ответа на вопрос.
Итак, я занялся детальным рассмотрением вопросов, возникающих в связи с
детерминированной доской Гальтона, поскольку никто раньше такими вопросам не задавался.
И попутно выявились боковые ходы, уводящие то в физику, например, найти энтропию
каждого из состояний переключтелей, или описать их состояние в терминах клеточных
автоматов, для того, чтобы лучше понять логику клеточных автоматов, чтобы, возможно,
сделать задачу нахождения произвольного состояния хотя бы элементарного клеточного
автомата вычислительно приводимой, за что, кстати, тот же Вольфрам обещает 30
американских килобаксов, или применить доску Гальтона для решения задачи коммивояжера,
за что уже институт Клея обещает один амеоиканский мегабакс.
Но это все, конечно шутка юмора, а вот то, что любой маршрут шарика по детерминированной
можно считать символом из каког-то алфавита, а весь цикл маршрутов - словом, составленным
из этих символов, (вспоминаем словарь Шарпера с доступом методом Трие), тогда
движение шариков по вероятностной доске можно представить таким же словом, только
закрытым линейным шифром, и здесь можно придумать много задач, типа представить
зашифрованное слово, образованное циклом маршрутов по вероятностной доске,
в виде суииы (побитовой?) нескольких открытых слов, образованных циклами маршрутов
шариков по детерминированной доске.
И это только первые мысли, которые мне взбрели в голову. На самом деле это кладезь
плодотворных идей.
Отредактировано Лукомор (2023-06-05 14:51:28)
Я выпилил виртуальным лобзиком системы Paint, щас буду фоткать процесс,
а зачем оно тебе, я не знаю...
Да мне тебя просто жалко, как ты рукопашно гравитацию заменяешь
Потом я вдруг понял, что детерминированную доску Гальтона до сих пор вообще
никто не изучал
Ну, наконец-то! О чем я и говорю с прошлого века! Замели под ковер кучу вопросов, объявив их тривиальными и не стоящими внимания! И получили популяцию пересчитывающих информацию в АВМ на биты и байты и всерьез рассуждающих о путешествиях во времени
И она благополучно проскользнула тогда мимо моего сознания, которое было поглощено
ыероятностной шахматной доской
Вот-вот! Именно это меня и выбешивает - увлечение модными штучками. Я этим увлекался в ВУЗе, полюбив теорвер, но чем дальше изучал техмаш, который весь основан на "борьбе с энтропией" методом загона случайности в заданный интервал, понял, что вероятностные методы совершенно непригодны в отношении самоорганизации, а вероятностные шахматы это чистый цефалокоитус. И в 1983 мне попался Вольфрам
Да мне тебя просто жалко, как ты рукопашно гравитацию заменяешь
Я не рукопашно, я вооружен... фотолобзиком!
Хотя, если честно, мне проще и нагляднее с единичками и ноликами, чем с этими мультиками.
А главное - в разы быстрее.
Но если заказчику надо картинки - мы можем и картинки.
Ну, наконец-то! О чем я и говорю с прошлого века! Замели под ковер кучу вопросов, объявив их тривиальными и не стоящими внимания!
Так я же выколупал из под ковра эту детерминированную доску, и торжественно тебе вручил!
И что?
Теперь самому придется все эти вопросы задавать и самому же на них отвечать....
И получили популяцию пересчитывающих информацию в АВМ на биты и байты
И скурпулезно пересчитывающих частоту в АВМ на биты и байты комбинаторных вариантов .
и всерьез рассуждающих о путешествиях во времени
И о детерминированности как в будущее, так и в прошлое.
И в 1983 мне попался Вольфрам
Здесь следуеет отметить, что за прошедшие с тех пор 40 лет Вольфрам добился
несколько больших успехов, видимо Шарпер на него сильнее повлиял.
Отредактировано Лукомор (2023-06-06 07:56:58)
Детерминированность напоминает идею бога
Детерминированность напоминает идею бога
«Бог не играет в кости!» - крылатая фраза Эйнштейна.
Отредактировано Лукомор (2023-06-06 07:57:44)
«Бог не играет в кости!» - крылатая фраза Эйнштейна
А как он объяснял появление Евы?
А как он объяснял появление Евы?
Про Еву никто Эйнштейна не спрашивал.
Да и сам тезис спорный. На что и указал Нильс Бор:
Фразу об игре в кости Эйнштейн повторял десятки раз.
Достойный ответ нашел Нильс Бор:
«Альберт, перестаньте, наконец, указывать богу, что ему делать!»
И только в начале 80-х появились документальные кадры 
(концовка фильма "Туз") где бог играет с Челентано в покер!
Так что Эйнштейн ы чем-то прав...
А как он объяснял появление Евы?
Реализация неизбежного события в цепи эволюционно связанных из ряда возможных альтернатив Вас устроит? Вероятностный метод даст вполне годный результат продемонстрировав всю мощь предсказательной силы метода, как на детерминированных доске Гальтона или клеточном автомате, не дав ничего полезного кроме диссертаций. Гад Вольфрам всю малину вероятностникам обломал, "а ведь было еще столько идей". (А куда колобки делись?)
Очевидно, что переключатель один, поэтому исходных состояний,
до пуска первого шарика всего два, Либо L-влево, как на рисунке в прошлом сообщении,
либо R-вправо, как вот здесь:
Если R, то первый, и все последующие шарики с нечетными номерами будут переключать
переключатель в положение L, а сами будут уходить по маршруту l в первый карман.
Соответственно второй, и все последующие шарики с четными номерами будут
переключать стрелку в положение R, и уходить по маршруту r во второй карман.
Отредактировано Лукомор (2023-06-07 01:24:35)
из ряда возможных альтернатив
А можешь перечислить все альтернативы из ряда возможных?
Отредактировано Лукомор (2023-06-07 01:47:47)
Хотя, если честно, мне проще и нагляднее с единичками и ноликами, чем с этими мультиками.
А главное - в разы быстрее.
Ну и хорошо, если не лень
И скурпулезно пересчитывающих частоту в АВМ на биты и байты комбинаторных вариантов .
Какую частоту? Помнишь ролик с кулачковой АВМ от 1948 года. Пытаются пересчитывать на биты
И о детерминированности как в будущее, так и в прошлое.
В упор не понимая, что не существует обратимых процессов, есть исключительно и только воспроизводимые, среди которых встречаются воспроизводимые в обратном порядке, типа воспроизведения записи в обратном направлении
Здесь следуеет отметить, что за прошедшие с тех пор 40 лет Вольфрам добился
несколько больших успехов, видимо Шарпер на него сильнее повлиял.
Да-да, конечно. Это ж классика -
Я вот тоже как-то за Вольфрама, нашего, Стивена, брался опосля работы у "металлорежующего станка".
А можешь перечислить все альтернативы из ряда возможных?
Нет. Это как перечислить все начальные комбинации клеточных автоматов с учетом их разнообразия.
Нет. Это как перечислить все начальные комбинации клеточных автоматов с учетом их разнообразия.
В этом слабость комбинаторно-цифрового подхода к понятию вероятности.
Для того, чтобы его реализовать, нужно сначала перечислить весь ряд возможных
альтернатив. И тут оказывается, что в конкретном случае возможных альтернатив,
который мы с подачи Доктора-нашего-Лектора выше разбирали,
про эволюционно-связанное неизбежное событие сотворения богом женщины,
мы можем вспомнить только две альтернативы: первая женщина была слеплена
из глины и палок, но тут же была признана неудачной попыткой, и вторая
уже, как положено, если не ошибаюсь, из девятого ребра Адама.
Но это не означает, что других альтернативных вариантов, нереализованных,
у бога в запасе не было.
А без знания всех альтернативных комбинаторных вариантов,
вероятность, которая в данном случае получается равной р=2,
не может быть вычислена правильно.
Это как перечислить все начальные комбинации клеточных автоматов с учетом их разнообразия
Ты невнимательно прочитал книгу Вольфрама "New kind of science"-, более чем полностью
посвященную клеточным автоматам. Впрочем тебе простительно, там более 1200 страниц,
и она не переведена на русский язык. 
Так вот там, как раз описано правило Вольфрама, которое позволяет перечислить все
без исключения элементарные клеточные автоматы.
А для любого конкретного элементарного клеточного автомата, с известным номером
правила Вольфрама, начальная комбинация состояний его клеток задается просто
двоичным числом, соответствующим данной начальной комбинации.
среди которых встречаются воспроизводимые в обратном порядке, типа воспроизведения записи в обратном направлении
Я уже говорил когда-то , что воспроизведение в обратном порядке неоднозначно,
по крайней мере для клеточных автоматов.
Для элементарных клеточных автоматов каждое текущее состояние будет иметь ровно
четыре различных предыдущих состояния, то-есть к данному ссостоянию всего за один
ход могут привести четыре совершенно различных предыдущих состояния.
При обратном воспроизведении для текущего состояния элементарного клеточного автомата
есть четыре альтернативных предыдущих состояния, и вероятность, что он будет возвращаться
тем же путем, которым пришел, равна Р=1/4.
Собственно и воспроизводимость в прямом направлении это тоже утопия.
Для подбрасываемлгл кубика, одно и то же тщательно повторенное сочетание начальных
условий даст непредсказуемый результат.
Отредактировано Лукомор (2023-06-07 08:20:10)
Помнишь ролик с кулачковой АВМ от 1948 года. Пытаются пересчитывать на биты
Не помню.
Зачем кулачковая АВМ что-то там пересчитывает на биты?
Ну и хорошо, если не лень
Мне не лень, но хорошо что:
Хорошо - картинки,
или
хорошо - цифровая нотация?
Ты совершенно невнятно выражаешься...
Так вот там, как раз описано правило Вольфрама, которое позволяет перечислить все
без исключения элементарные клеточные автоматы.
Ты случаем правило с кодом не путаешь, родной? C тем, который придуман для поименования КА? И еще, чисто любопытно, под перечислением ты что имеешь в виду?
Не помню.
Зачем кулачковая АВМ что-то там пересчитывает на биты?
Не она, а для нее
Вы здесь » Амальгама » Лукоморье 2.0 » Доска Гальтона и связанный с нею парадокс