Интересно, а что будет, если у доски склеить вертикальные края и сделать из неё цилиндр?
Доска Гальтона и связанный с нею парадокс
Сообщений 31 страница 60 из 670
Поделиться322023-05-10 16:28:09
Интересно, а что будет, если у доски склеить вертикальные края и сделать из неё цилиндр?
Это очень интересный случай, но для этого доска должна быть сразу пряямоугольной.
Я начал с простого случая, с треугольной доки Гальтона.
Для прямоугольной будет несколько разных вариантов,
в зависимости от ширины исходной доски.
В самом интересном случае будет равномерное распределение вариантов:
1. 1. 1 .... 1. 1. 1
. 2 2 2..2 2 2
....4 4 .. 4 4 4
8 8 8... 8 8
Поделиться332023-05-10 17:21:09
Я начал с простого случая, с треугольной доки Гальтона.
Я пока не вижу отличий от доски типа "сортировочная горка". Если такой пока не было, то пусть будет имени меня, чем я хуже того Гальтона:
Каждый шпенёк заменён на стрелочный перевод. Путь вниз фиксирован и направлен на одного из потомков в нижнем слое. При прохождении шарика стрелочный перевод меняет направление.
И есть у меня сильное подозрение, что у доски Гальтона и горки Доктора результаты на большом числе шариков отличаться не будут...
Поделиться342023-05-10 17:58:05
В самом простом случае, когда доска Гальтона имеет форму треугольника и в каждой точке ветвления любой шарик с вероятностью р=1/2 после этой точки ветвления может отклониться влево или вправо.
А вариант с переключателями вместо штырей не рассматривается?
Поделиться352023-05-10 18:08:10
А вариант с переключателями вместо штырей не рассматривается?
Каждый шпенёк заменён на стрелочный перевод. Путь вниз фиксирован и направлен на одного из потомков в нижнем слое. При прохождении шарика стрелочный перевод меняет направление.
Рассматривается, но разницы особой нет.
Получается то же самое биномиальное распределение, и это не удивительно.
В каждом узле ветвления происходит разделение на два потока,
половина шариков уходит налево, половина - направо.
Вот кстати, горка "докторская", я ее уже выкладывал ранее:
Отредактировано Лукомор (2023-05-10 18:23:32)
Поделиться362023-05-11 09:06:20
Я пока не вижу отличий от доски типа "сортировочная горка". Если такой пока не было, то пусть будет имени меня, чем я хуже того Гальтона:
От радости я даже не буду предъявлять претензий за попытку плагиата с имени меня на имени Вас! Просто поздравлю с долгожданным принятием неизбежного выбора пути самурая эээ ... интегрирующей кошки ... бегемота?.. О! стрелочника, который ведет к победе коммунистического труда
пониманию принципа различения объектов окружения
Поделиться372023-05-11 09:09:14
В каждом узле ветвления происходит разделение на два потока,
половина шариков уходит налево, половина - направо.
Ишь ты, на два... А можно зависимость усложнить с учетом состояния соседей
Поделиться382023-05-11 09:36:21
А можно зависимость усложнить с учетом состояния соседей
Можно... но потом...
Потому что чудеса наступают не только с усложнением взаимовлияния шариков друг на друга, но и с изменением геометрической формы самой доски Гальтона, чем мы и займемся буквально сейчас, после небольшого перекура...
Поделиться392023-05-11 13:49:50
можно зависимость усложнить с учетом состояния соседей
Отличная идея!
*прикидывает перекрёстную схему соединения аппаратов ИВЛ и кардиомониторов в реанимации*
Поделиться402023-05-11 13:51:53
пониманию принципа различения объектов окружения
Да тут всё просто. Вечером в пятницу понятны любые принципы и объекты. Утром в субботу холодный рассол ситуация обратная.
Поделиться412023-05-11 18:08:22
Да тут всё просто. Вечером в пятницу
Так... Сегодня у нас четверг... Я подожду.
Поделиться422023-05-11 22:43:41
Я подожду.
Я извиняюсь...
"Меня отвлекали!" (с) Рома Березуев (на Сайлоге).
Но вот вам обещанные чудеса с геометрией доски Гальтона.
Разумеется, с последующим их полным разоблачением,
как некогда в театре "Варьете" у Булгакова.
Итак, мы возьмем треугольную доску Гальтона,
и с некоторого уровня установим вертикальные перегородки,
так, что получится домик с вертикальными стенами и треугольной крышей.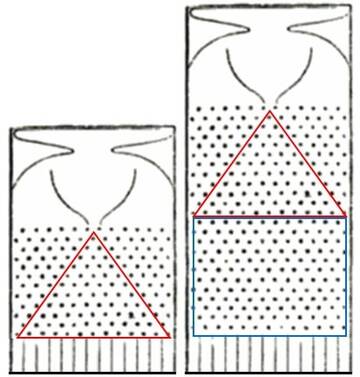
Ну, для примера, я возьму пять уровней треугольной доски,
и далее ее ширина меняться не будет.
Вначале посчитаем количество различных возможных маршрутов шарика
в каждую точку ветвления. Разумеется, для вертикальной части доски ,
это количество уменьшится,
по сравнению с соответствующим слоем доски треугольной,
поскольку часть маршрутов обрежется.
Так в шестом слое их будет 30, вместо 32.
В седьмом слое -60, вместо 64, и этот дефицит маршрутов
будет возрастать от слоя к слою в геометрической прогрессии.
Найдем процент количества маршрутов в каждую точку ветвлениея,
по отношению к общему количеству маршрутов для данного слоя:
Для точек В6 и Н6 на картинке, это будет 5/30 = 1/6
Для точек D6 и F6 - 10/30 = 1/3
A7 и I7 = 5/60 = 1/12
С7 и G7 =15/60 = 1/4
Е7 = 20/60 =1/3
Отредактировано Лукомор (2023-05-11 23:47:44)
Поделиться432023-05-11 23:23:23
Теперь зайдем с другой стороны, и посчитаем вероятности, что шарик,
выйдя из верхней точки, окажется в конкретной точке конкретного слоя.
При этом учтем, что в отличие от различных маршрутов, которых уменьшается,
число шариков вышедших из верхней точки, не уменьшается, поскольку
часть шариков отражается от вертикальных стенок, и продолжает
свое движение по уже перечисленным маршрутам.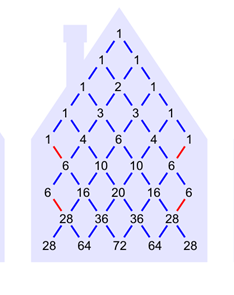
Теперь возьмем те же точки шестого и седьмого слоя, до которых
уже посчитан процент различныз маршрутов, и найдем вероятности того,
что случайно блуждающий шарик окажется в этой же точке ветвления.
Р(В6)=Р(Н6)= 6/32 =3/16
Р(D6)=P(F6)=10/32 = 5/16
P(A7)=P(i7)= 6/64 = 3/32
P(C7)=P(G7) = 16/64 = 1/4
P(E7) = 20/64 = 5/16
Кое-где значения совпадают, но в основном - не бъют...
Отредактировано Лукомор (2023-05-13 11:33:11)
Поделиться452023-05-12 12:05:19
А вот это Шарперу в копилочку:
Нафиг мне пинг-понг? Это же модель неисправного фильтра - с внутренними искажениями
Поделиться462023-05-12 12:15:23
ще движнгтн шарика
Это же модель неисправного фильтра - с внутренними искажениями
Ну, нормальная доска Гальтона, не битая, а так... под ремонт... 
И вообще, кто сказал, что доска Гальтона - это фильтр?
Это ты еще не видел движение шарика по доске Гальтона в невесомости! 
Отредактировано Лукомор (2023-05-12 12:18:03)
Поделиться472023-05-13 10:19:56
Итак, при движении шариков у нас получилось
два разных распределения случайной величины.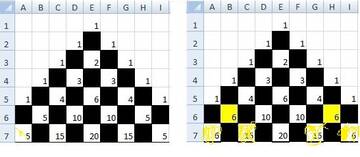
На левом рисунке наука комбинаторика перечисляет нам
все возможные различные маршруты шарика
от верхней ячейки Е1 до каждой из ячеек нижних уровней.
На правом рисунке наука теория вероятностей рисует нам
количество шариков, которое проходит через каждую ячейку.
Начиная с шестого ряда бухгалтерия перестает сходиться,
и нам нужно:
во-первых, найти этому рациональное объяснение
во- вторых изыскать возможность свести эти две картинки в одну,
и объяснить, "почему сие важно в-третьих"(с) Куприн "Поединок" 
В первом приближении объяснение будет таким:
Поскольку стенки, установленные вертикально внутри треугольной доски Гальтона
обрезают часть маршрутов, которые в треугольной доске проходят вне
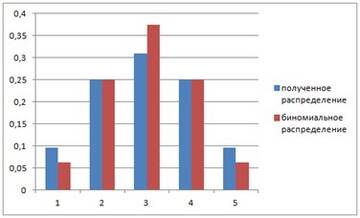
новых границ, то процент оставшихся маршрутов пропорционально возрастает,
особенно это заметно в центральных ячейках (красные столбцы на графике),
Но сами шарики, отражаясь от стенок, повторяют
некоторые из уже проложенных маршрутов, и, поэтому,
вероятность нахождения шарика в ячейке растет прежде всего по краям доски.
Это заметно на синих столбцах графика.
Шарпер сказал бы, что "маршруты возле стенок лучше протаптываются,
за счет прохождения по ним, дополнительно, шариков, отраженных от стенок ".
Действительно, если из узла выходит две синих "тропинки" то вероятность ,
что шарик пойдет по любой из них равна 1/2, но из крайних узлов выходит
лишь одна тропинка (красная) и шарик пойдет по ней с вероятностью
вдвое большей,то-есть, попросту равной 1.0, поскольку вариант есть всего один.
Таким образом по этим красным тропинкам протопчется вдвое больше шариков,
за сравнимое время, чем по синим.
Так мы ответили на вопрос : " Кто виноват?".
Виновата, как всегда, - стенка, и нам надо как-то свести эти два случая
к общему распределению.
И на вопрос :"Что делать?" - в сложившейся ситуации, есть несколько способов
ответить.
Отредактировано Лукомор (2023-05-13 11:45:11)
Поделиться482023-05-15 05:48:40
вероятность нахождения шарика в ячейке растет прежде всего по краям доски.
И что тут удивительного ? Если эта доска постоянной ширины продолжится достаточно долго то вероятность нахождения шариков будет приближаться к какому-то одинаковому значению по всей ширине.
Поделиться492023-05-15 07:09:18
Шарик для пинг-понга на доске Гальтона
Задача пьяного коммивояжера
Поделиться502023-05-15 11:35:31
И что тут удивительного ?
Если эта доска постоянной ширины продолжится достаточно долго то вероятность нахождения шариков будет приближаться к какому-то одинаковому значению по всей ширине.
Я даже больше скажу, количество неповторяющихся маршрутов тоже имеет
тенденцию к выравниванию по всей ширине, с увеличением высоты доски Гальтона
(количества слоев на которых маршруты разделяются).
И в этом ничего нет удивительного, поскольку с центрального ряда шарики уходят
влево/вправо, а им на смену приходит маньшее количество шариков,
поскольку из ряда соседнего с центральным тоько половина шариков возвращается,
а вторая половина уходит еще дальше от центра.
.
Удивительно тут то, что относительное число различных маршрутов через данную
точку ветвления и вероятность того, что шарик окажется в данной точке на своем пути,
имеют разную физическую природу, и сообразно с этим отличается динамика
их движения к равновесному состоянию.
Так, например, количество возможных маршрутов через данную точку постоянно
урезается краями доски. И прирастает только за счет маршрутов, пришедших в крайнюю
точку из центральных областей.
Это образно можно представить в виде кучи песка, из которой песок забирается с краев,
и куча из-за этого постепенно проседает под собственным весом.
Другое дело вероятность того, что шарик во время спуска по доске оказался
в данной точке ветвления. Дело в том, что в отличие от маршрутов из крайней точки,
от стенки, которых только один, количество шариков, выходящих по этому единственному маршруту -
удваивается, поскольку один шарик в этой точке и так ушел бы к центру, а второй
должен был бы уйти еще дальше от центра, но встретил на своем пути стенку, отразился
от нее и также ушел в направлении центра доски.
Один маршрут, но по нему идут два шарика, прямой и отраженный.
Так количество маршрутов от стенки остается прежним, а количество шариков
проходящих по этим маршрутам, при подсчете удваивается.
Это можно сравнить с той же кучей песка, из которой песок не забирают, а наоборот,
досыпают его с краев.
Из-за чего превышение верхней точки кучи над уровнем песка на краях уменьшается.
Теперь, если мы возьмем отношение числа маршрутов через данную точку,
к общему числу маршрутов на данном уровне (слое) и обозначим ее Q,
а вероятность того, что шарик на данном уровне окажется в той же точке
обозначим P, то отношение k=P/Q
окажется существенно выше, на краях, и незначительно выше в центральных областях.
причем еще и будет рости по краям гораздо быстрее, чем в центральных областях,
от слоя к слою.
В терминах Шарпера, маршруты на краях доски протаптываются гораздо интенсивнее,
чем в центральных областях, шарики гораздо охотнее топчутся по краям доски.
Механик, возможно, сказал бы, что на шарики действует некая
загадочная центробежная сила, увлекающая их от центра доски к краям.
Вот это и парадоксально, хотя, с учетом сказанного выше, не удивительно.
И наша задача в этом парадоксе разобраться до конца.
Отредактировано Лукомор (2023-05-15 11:45:09)
Поделиться512023-05-15 12:09:36
Задача пьяного коммивояжера
Говорят, что "в каждой шутке есть доля шутки" 
В данном, шутливом по форме, замечании, на самом деле скрыт глубокий смысл.
Действительно, разгадка сформулированного выше парадокса доски Гальтона,
находится несложно, если привлечь достаточно хорошо проработанное в теории
вероятностей понятия:"случайное блуждание", которое описывает и
броуновское движение частиц в физике, и колебания курсов акций на бирже,
и движение пьяного коммивояжера, и полет пьяного Карлсона... 
Этим мы сейчас и займемся...
Поделиться522023-05-15 12:28:16
А что где - то есть сформулированный парадокс доски Гальтона ?
Поделиться532023-05-15 13:00:15
А что где - то есть сформулированный парадокс доски Гальтона ?
Нету!
Впервые он сформулирован в этой теме, на форуме Амальгама.
/*Ха! Стал бы я писать о том, что уже где то есть сформулированное....
Отредактировано Лукомор (2023-05-15 14:48:52)
Поделиться542023-05-16 19:23:52
вот имена у нас с ним были одинаковы. Это меня несколько поразило - вроде не принято было давать имена умерших братьяв
Ну не знаю , у мамы были первые двое близнецы, Михаил и Александр. Александр простыл. воспаление легких, в 49, да еще для 3 летнего , это ...
В 59 я родился тоже назвали Александром, ни чего жив до сих пор.
Поделиться552023-05-17 10:02:44
Впервые он сформулирован в этой теме, на форуме Амальгама.
И где ?
Поделиться562023-05-17 11:22:29
И где ?
Сейчас уже сформулирую! 
Точнее, строгой формулировки, в классическом виде : "вот истинное утверждение,
отрицание которого тоже есть истина." - не будет.
Вся эта тема выросла из обсуждения совсем другого вопроса
на более другом форуме семь лет назад.
И там она была не основной, изначально там рассматривлся просто вопрос выравнивания
вероятностей нахождения шарика в некоторой точке ветвления
на прямоугольной доске Гальтона с увеличением количества ее уровней.
И все было чинно- благородно, и вероятности считались с учетом отражения шарика от
боковых вертикальных стенок, но пришел некий персонаж, и, размахивая классической
книгой Н.Я. Виленкина "Комбинаторика" начал всем рассказывать,
что вероятности мы считаем неправильно.
Потому что, вот же, в книге есть задача о количестве различных маршрутов шашки
по шашечно-шахматной доске (рисунок из книги). 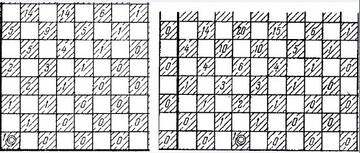
И различных маршрутов этих гораздо меньше,
чем вы тут себе нафантазировали, а поскольку прямоугольная доска Гальтона
моделирует как раз движение шашки по шахматной доске, то извольте
считать вероятности по книжному!
Вот, собственно, сюжетная линия, где нет парадокса, но парадоксальна сама ситуация,
где никакие аргументы на персонажа не действует, и в результате более чем годичного (!)
обсуждения удалось наглядно показать:
во-первых, что для иллюстрации именно движения шашки по шахматной доске
обсуждаемая модель лоски Гальтона не подходит вообще, а нужна доска Гальтона
той же формы, но совершенно иной конструкции - это было прсто;
и, во-вторых, в той изначальной доске Гальтона, которая вообще не подходит,
найти и показать наглядно именно те недостающие маршруты, которых
"не видно, но они есть". Это также не сложно, но нужно немножко смекалки.
То-есть, оставаясь в рамках неправильной модели, найти правильный ответ
на правильно поставленный вопрос.
Отредактировано Лукомор (2023-05-17 11:30:38)
Поделиться572023-05-17 13:22:19
Да хрен с ней с историей. Никак не пойму, что хорошо и что плохо, какова последовательная формулировка парадокса доски Гальтона и каково последовательное описание именно той доски о которой идет речь.
Поделиться582023-05-17 17:24:00
каково последовательное описание именно той доски о которой идет речь.
Это вопрос сложный, поскольку в том давнем обсуждении описание менялось каждый раз, когда топикстартеру не нравилось очередное решение.
То - есть, было решение, под которое никак не удавалось подогнать условия задачи.
Поэтому, доска Гальтона из треугольной приобрела форму "домика"
с верхней треугольной и нижней прямоугольной частью.
Цифирь для этого варианта я выкладывал выше. Следующий вариант,
который мне хотелось бы здесь и сейчас рассмотреть, оказался последним,
дальше дрейфовать было некуда.
Сначала это шахматная доска, 8х8 клеток, по черным клеткам , случайным образом,
двигается шашка, прокладывая случайный маршрут от первой горизонтали до восьмой.
На одну из четырех черных клеток первого ряда шашка также выставляется
случайно и равновероятно.
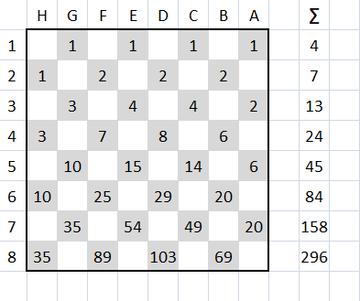
Подсчет количества различных маршрутов, проходящих через каждую клетку,
прилагаю.
/* Доска развернута на 180 градусов, для однообразия с соответствующей
доской Гальтона, где первый ряд вверху, а последний - внизу.
Аероятности, посчитанные двумя разными рассуждениями - отличаются,
в этом есть нечто парадоксальное...
или нет?
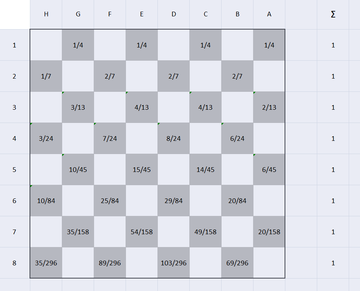
Понятно, что случайный маршрут шашки проходит ровно через одну клетку каждого ряда,
и взяв отношние количества различных маршрутов шашки через данную клетку,
к суммарному количеству различных маршрутов в данном ряду,
получим вероятность прохождения случайной шашки через данную клетку.
Вот я нарисовал эти вероятности уже:
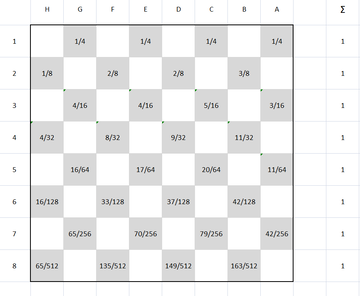
Теперь соорудим прямоугольную доску Гальтона в форме шахматной доски,
где будет столько же уровней, и столько же узлов ветвления, как и у шахматной доски и,
что самое главное, в крайних узлах ветвления шарик, попавший на край,
будет с вероятностью 1.0 отражаться внутрь доски. С учетом этого упрямого факта,
снова посчитаем вероятности прохождения шарика через каждый узел,
соответствующий клетке шахматной доски:
Отредактировано Лукомор (2023-05-17 19:07:19)
Поделиться592023-05-17 21:20:44
какова последовательная формулировка парадокса доски Гальтона
Мы посчитали двумя разными способами вероятность прохождения маршрута через данную точку ветвления маршрута, и получили два разных результата.
Парадокс?! Нет, но нечто парадоксальное видится в этои во всем....
Поделиться602023-05-17 21:22:58
что хорошо и что плохо
Плохо то, что подобные вопросы возникают периодически,
хорошо, что на все вопросы найдены ответы.