Ух ты, чо нашел! Еще на Мембрании ссылался, но прочно потерял.

ДНК - основа вычислительных машин
(203-204)29-30`1999
Влад Борисов | 10.08.1999

Генетические компьютеры способны выполнять триллионы операций в секунду

Мы все привыкли думать, что компьютер должен состоять из микросхем, накопителей на жестких дисках и магнитных лентах, монитора и тому подобных деталей. Однако идея, предложенная в 1994 г. известным криптографом Леонардом Адельманом (Leonard Adleman), одним из авторов алгоритма шифрования с открытым ключом RSA, грозит сделать такое представление несколько устаревшим - ведь к традиционным “железякам” вскоре могут добавиться колбы и пробирки, в которых будут производиться вычисления на базе молекул дезоксирибонуклеиновой кислоты - ДНК. В одном литре вещества может находиться до 1017 этих молекул, каждая из которых, как мы увидим, представляет собой небольшой компьютер. Суммарная производительность всей этой массы нанокомпьютеров, работающих параллельно, может в тысячи раз превосходить производительность современных кремниевых систем.

Биологические аналоги компьютерных систем

Фундаментом всей системы хранения биологической информации, а стало быть, и ДНК-компьютеров, является способность атомов водорода, входящих в азотистые соединения аденин (Adenine, A), тимин (Thymine, T), цитозин (Cytosine, C) и гуанин (Guanine, G), при определенных условиях притягиваться друг к другу, образуя нехимически (т. е. невалентно) связанные пары A = T и C є G.

С другой стороны, эти вещества (или, как еще говорят, основания) могут валентно связываться с фосфатно-дезоксирибозными группами - комбинациями молекулы сахара (дезоксирибозы) и фосфата, образуя так называемые нуклеотиды (рис. 1). Нуклеотиды, в свою очередь, легко образуют полимеры длиной в десятки миллионов оснований. В этих супермолекулах фосфат и дезоксирибоза играют роль поддерживающей структуры (они чередуются в цепочке), а азотистые соединения кодируют информацию. Молекула получается направленной - она начинается с фосфатной группы и заканчивается дезоксирибозой. Длинные цепочки ДНК называют нитями (strands), а короткие - олигонуклеотидами.

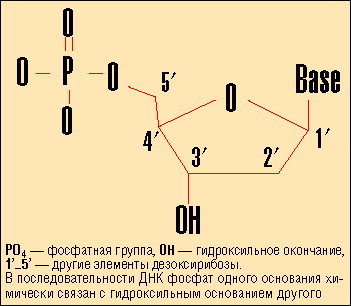
Рис. 1. Структура нуклеотида

Каждой молекуле ДНК соответствует еще одна ДНК - так называемое дополнение Ватсона - Крика (Watson-Crick complementary). Она имеет противоположную направленность, нежели оригинальная молекула, и получается из последней заменой оснований A, T, C, G на парные к ним. В результате притяжения аденина к тимину и цитозина к гуанину получается знаменитая двойная спираль, обеспечивающая возможность удвоения числа ДНК при размножении клетки.

Задача удвоения решается с помощью специального белка (энзима) - полимеразы. Этот энзим скользит вдоль ДНК и синтезирует на ее основе новую молекулу, в которой все основания заменены на соответствующие парные. Интересно, что синтез начинается только в том случае, если к ДНК прикреплен коротенький кусочек ее дополнения (или “зацепки” - primer). Данное свойство активно используется в молекулярной биологии и молекулярных вычислениях.

По сути своей полимераза - это реализация машины, придуманной в тридцатых годах выдающимся британским математиком Тьюрингом (машина Тьюринга, МТ), которая состоит из двух лент и программируемого пульта управления. Пульт считывает данные с одной ленты, обрабатывает их по некоторому алгоритму и записывает их на другую ленту.

Полимераза также последовательно считывает исходные данные с одной ленты (ДНК) и на их основе формирует ленту с результатом вычислений (дополнение Ватсона - Крика). С теоретической точки зрения, запрограммировав пульт, можно заставить МТ делать что угодно - играть в шашки, строить прогноз экономического развития Зимбабве до 3071 года или подсчитывать декалитры выпитой водки. Природа, правда, снабдила нас устройствами, решающими ограниченный круг задач, но именно подобие полимеразы и МТ навело Адельмана на мысль о возможности построения вычислительных систем на базе ДНК.

В живых организмах полно других аналогов машины Тьюринга. Например, энзим транскриптаза считывает ДНК и синтезирует на ее основе молекулу рибонуклеиновой кислоты (РНК*1). Другой энзим - обратная транскриптаза - транслирует РНК в ДНК. Именно он является основой жизнедеятельности самых зловредных вирусов - ретровирусов (к ним относятся вирусы гриппа и ВИЧ), которые не имеют собственной ДНК (только РНК) и при помощи этого приводят свое описание в “формат”, подходящий для включения в ДНК клетки. Затем вирус запускает механизм размножения клетки, размножающий теперь и его самого. В качестве долговременного хранилища информации РНК по причине низкой надежности в организмах используются редко.

_____

* РНК отличается тем, что в ней дезоксирибоза заменена на другой сахар (рибозу), а тимин - на урацил (Uracil, U).

В процессе считывания данных из ДНК в РНК (трансляции) получается так называемая “РНК с сообщением” (message RNA), передаваемая на вход рибосомы (синтезатора белков из аминокислот) - еще одного аналога машины Тьюринга. Белок в рибосоме играет роль выходной ленты - для его конструирования обычно требуются тысячи аминокислот, каждая из которых кодируется последовательностью из трех оснований. Сами аминокислоты рибосома различает по присоединенным к ним “биркам”, или “транспортным” РНК, также состоящим из трех оснований. Необходимость трансляции объясняется тем, что читать напрямую из ДНК информацию, нужную для синтеза белка, опасно, так как вероятность повредить эту молекулу при подобной часто повторяющейся операции весьма велика. Вся идея синтеза РНК из ДНК - классический пример кэширования.

Классы сложности математических проблем

Если вы устали читать о биологии, то самое время вернуться к математике. Какие задачи можно решить с помощью ДНК и как это делать? И какую задачу выбрать на первый раз? Прежде всего стоит вспомнить о главном предполагаемом преимуществе молекулярных вычислений - огромной параллельности. А это значит, что для “показательных выступлений” задача должна быть достаточно сложной для современных компьютеров и в то же время хорошо распараллеливаемой.

Трудность задачи в комбинаторике определяется временем, необходимым для ее решения на детерминированной и недетерминированной машинах Тьюринга (ДМТ и НДМТ). Эти воображаемые устройства принципиально отличаются друг от друга. ДМТ исполняет детерминированные алгоритмы: в них все операции выполняются последовательно и предопределены заранее. Примером может служить сложение векторов.

НДМТ, напротив, исполняет недетерминированные алгоритмы. В них имеются узловые точки, где производится выбор направления дальнейших действий из некоторого множества возможных вариантов. Рассматриваемая в теории сложности НДМТ может создавать в каждой узловой точке новые копии самой себя в количестве, равном числу ветвлений алгоритма. Дальнейшие вычисления производятся этими копиями параллельно. Забегая вперед, скажу, что в молекулярных вычислениях используется самый простой вариант этой машины - вначале создается исчерпывающее множество всех возможных решений (включая неверные), затем система их проверяет в режиме параллельных вычислений, отбирая лишь те, которые действительно решают поставленную задачу.

На основании того, известен или нет для данной задачи эффективный алгоритм для ДМТ и НДМТ, выделяют классы сложности P, NP, NP-complete (NPC). К типу P (polynomial) относятся задачи, решаемые на ДМТ за полиномиальное время, т. е. за время порядка ns, где n определяет масштаб задачи (скажем, длину ключа шифрования или количество вершин графа), а s - некоторое число, характеризующее алгоритм. К NP (nondeterministic polynomial) относятся задачи, которые решаются за экспоненциальное время на ДМТ (т. е. за время порядка s^n) и за полиномиальное время на НДМТ. Такой, например, является задача разложения числа на простые множители, на трудности которой базируется алгоритм RSA.

Естественно, что любая задача, относящаяся к P, относится и к NP (рис. 2), ведь каждый детерминированный алгоритм можно рассматривать как недетерминированный, но с одним вариантом выбора в том или ином узле. Поэтому НДМТ может решить за полиномиальное время задачу, на которую ДМТ потребуется экспоненциальное время.

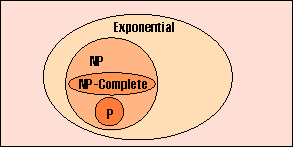
Рис. 2. Современные представления о классах

сложности математических задач

Заметим, что оценка сложности задач - вещь непостоянная. Она основана на текущем НЕЗНАНИИ эффективного алгоритма решения проблем на детерминированной машине. Не факт, что такие алгоритмы не появятся в будущем. Иначе говоря, классификация задач во многом - вопрос веры. Математически не доказано, что множество NPP не пусто, т. е. что существует хотя бы одна проблема, входящая в NP и не входящая в P.

Математик Стивен Кук показал в 1971 году, что в NP существует подмножество задач, обладающих интересным свойством: если находится детерминированный полиномиальный алгоритм для одной из них, то должны существовать аналогичные алгоритмы для всех задач NP, т. е. P = NP. Кук назвал этот класс NP-complete (NPC). Все входящие в него задачи эквивалентны с вычислительной точки зрения, и можно показать, что за полиномиальное время любая проблема из NP сводится к NPC-проблеме. NPC-задачи считаются наиболее сложными в NP, и математики верят, что для этих задач полиномиальных детерминированных алгоритмов уж точно не существует. К NPC-задачам относятся, например, проблемы отыскания Гамильтонова пути (иначе - задачи коммивояжера) и “собирания набора рюкзаков” (knapsack problem, KP). На КР основан криптографический алгоритм Меркли и Хелмана (Merkle&Hellman) и ряд других шифров.

Практическая же важность проблем NP в том, что на детерминированной машине они перестают быть физически решаемыми при n гораздо меньшем, чем у задач класса P. Этот принцип широко используется в современной криптографии. Между тем новые типы вычислительных машин - квантовые и молекулярные компьютеры - являются ограниченными реализациями НДМТ и теоретически способны решать NP-проблемы за полиномиальное время.

Эксперимент Адельмана

Для доказательства возможности вычислений на базе ДНК Адельман выбрал проблему отыскания Гамильтонова пути графа (Leonard M. Adleman, Molecular Computation of Solutions to Combinatorial Problems, Science, № 266/94, с. 1021). Суть ее в следующем. Имеется граф с n вершинами, соединенными однонаправленными ребрами. Нужно найти путь из одной заданной вершины в другую, проходящий через все остальные вершины только один раз, или доказать отсутствие такого пути. Задача дискретная, решать ее можно лишь перебором, она имеет прикладное значение (к ней можно свести задачу разложения числа на множители), и все существующие для нее детерминированные алгоритмы имеют экспоненциальное время исполнения.

Для решения задачи Адельман воспользовался следующим недетерминированным алгоритмом:

1. Сгенерировать все возможные варианты путей через граф.

2. Исключить все пути, которые не проходят через заданные начальную и конечные вершины.

3. Исключить те пути, что проходят через число вершин, отличное от n.

4. Исключить все пути, которые проходят через какую-либо вершину по нескольку раз.

5. Если после этого хотя бы один путь остался, то это именно тот, что нужен.

Весь фокус в том, как заставить алгоритм работать. Даже для небольшого графа число возможных вариантов пути оказывается колоссальным! И здесь на помощь приходят молекулы.

В основе рассуждений Адельмана лежала возможность закодировать каждую вершину графа (рис. 3) уникальной последовательностью олигонуклеотидов A, T, C, G, например вершине O поставить в соответствие последовательность TATCGGATCGGTATATCCGA, O - GCTATTCGAGCTTAAAGCTA, O - GGCTAGGTACCAGCATGCTT и т. п. (в первоначальном эксперименте использовалась 20-разрядная кодировка). Тогда путь от одной вершины к другой можно определить как вектор из 10 последних оснований начальной вершины и 10 первых оснований конечной вершины, т. е. OO = GTATATCCGAGCTATTCGAG, OO = CTTAAAGCTAGGCTAGGTAC и т. д.

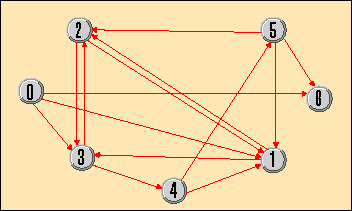
Рис. 3. Пример графа, взятый из статьи Адельмана

Как будет видно в дальнейшем, нужны еще дополнения Ватсона - Крика к молекулам Oi. Мы будем обозначать их ^Oi. Скажем, ^O2 = CGATAAGCTCGAATTTCGAT. Синтезировать все эти ДНК на современной биомолекулярной аппаратуре проще простого. Есть даже коммерческие фирмы, которым достаточно послать написанную на бумажке последовательность оснований, а на следующий день они уже пришлют пробирки с синтезированными молекулами.

Шаг 1. Для того чтобы алгоритм заработал, одних ДНК мало. Нужно прибегнуть к другим химикатам, изобретенным живой природой. Одним из них является лигаза, которая валентно склеивает разрывы в двойной спирали ДНК.

Если смешать раствор, содержащий ДНК, кодирующие ребра графа, с раствором, содержащим дополнения Ватсона - Крика для ДНК, кодирующих вершины, то за счет взаимного притяжения олигонуклеотидов в парах A - T и G - С 10-разрядное начало молекулы O2O3 притянется (с образованием двойной спирали) к концу молекулы ^O2, а конец O2O3 - к началу ^O3. Лигаза же найдет разрыв между ^O2 и ^O3, склеит его, объединив в результате две разных молекулы в одну.

То же самое произойдет и с другими ДНК, и если их достаточно много, то мы получим множество длинных двойных спиралей, кодирующих все возможные пути в Гамильтоновом графе! (По крайней мере, вероятность этого достаточно высока - молекул может быть миллиарды миллиардов штук.) Среди них есть и один путь, являющийся решением рассматриваемой проблемы. Но как его выделить среди массы ненужных путей?

Шаг 2. Найти иголку в стоге сена непросто, но если иголка вдруг начнет размножаться, то одинаковых иголок вскоре станет больше, чем сена. Именно эта идея и используется на втором шаге алгоритма.

В молекулярной биологии для увеличения числа ДНК применяется метод, называемый Polymeraza Chain Reaction (PCR, цепочечные реакции полимеразы; про полимеразу см. выше). При использовании этого метода раствор, содержащий двойные спирали ДНК, полимеразу, нуклеотиды A, T, G, C и молекулы “зацепок”, попеременно нагревается и охлаждается. При нагревании каждая двойная спираль распадается на две ДНК, а при охлаждении эти ДНК сначала рекомбинируют с “зацепками”, а затем рекомбинировавшие спирали восстанавливаются полностью при помощи полимеразы. Таким образом, правильно подбирая концентрацию веществ, можно добиться удвоения числа нужных молекул ДНК за один цикл нагревания/охлаждения.

В нашем случае “зацепками” нужно сделать O0 и ^O6. Тогда в PCR-циклах молекулы, содержащие начальные и конечные вершины (в том числе отражающие решение задачи), будут размножаться экспоненциально быстро, содержащие только одну их этих вершин - линейно, а остальные не будут размножаться вовсе. Иголок станет вскоре больше сена!

Шаг 3. На этом этапе молекулы фильтруются по длине: нужно оставить только ДНК длиной ровно 140 оснований. Делается это при помощи электрогелевого метода, аналогов которому в живой природе нет: ДНК помещаются в гелевый раствор и к нему прикладывается электрическое поле. Молекулы разной длины по-разному поляризуются и ускоряются в электрическом поле. В итоге одни молекулы движутся быстрее других, и через некоторое время ДНК разной длины можно разделить даже визуально - участки геля с ними видны как темные полосы. Аппаратура же позволяет разделять их с точностью до одного основания.

Повторяя несколько раз шаги 2 и 3, можно получить раствор, содержащий только молекулы, обладающие нужными свойствами.

Шаг 4. Как гарантировать, что граф проходит через все вершины? Оказывается, это можно сделать с помощью магнита. Методы молекулярной биологии позволяют прицепить к молекуле ДНК крошечный металлический шарик. Если такой молекулой является ^O2, то будучи добавлена в раствор, содержащий решение проблемы коммивояжера, она образует двойную спираль с какой-нибудь ДНК, кодирующей путь, проходящий через вершину 2. Если затем приложить к стенке сосуда с раствором магнит, то данная двойная спираль через некоторое время приплывет к этой стенке. Когда в раствор добавлено много молекул с железными шариками, то выход нужных ДНК будет большим. Если произвести подобную фильтрацию последовательно для всех вершин, то останутся только ДНК, содержащие решение проблемы!

Шаг 5. Победа! Осталось только размножить результат PCR-методом и определить последовательность оснований с помощью типовой машины секвенсирования (sequencing machine), используемой в молекулярной биологии. Если ни одной молекулы не нашлось, значит с большой долей вероятности можно утверждать, что для данного графа Гамильтонова пути не существует.

На выполнение всех этих операций у Адельмана ушло в 1994 г. семь рабочих дней. Самым трудоемким оказалось разделение молекул с помощью магнита. Вскоре другие авторы показали, как, используя аналогичный алгоритм, решать задачу Гамильтона для ребер, обладающих весом, - для этого вес нужно задавать целым числом и кодировать его в ДНК, повторяя нужное число раз последовательность, отображающую исходящую вершину ребра.

Бинарные задачи

Что еще можно делать с помощью ДНК? Ограничено ли поле деятельности таких машин комбинаторными проблемами? Оказывается, нет. Вскоре после опубликования работы Адельмана разные группы начали исследования в области решения логических задач.

В 1995 г. Ричард Липтон из Принстонского университета показал (Richard J. Lipton, DNA solution of hard computational problems, Science, № 268/95, с. 542), как, используя ДНК, кодировать двоичные числа и решать проблему удовлетворения логического выражения. Суть этой проблемы состоит в следующем. Пусть имеется некоторое логическое выражение F(X1, X2, ...., Xn). Какие значения нужно присвоить входящим в него логическим переменным Xi, чтобы F давало истину?

Вообще говоря, задачу можно решить только перебором 2^n комбинаций. И с помощью ДНК легко закодировать их все. Для этого нужно построить граф, описывающий операцию присваивания значений переменным. В нем вершины отображают единичные и нулевые значения Xi, некоторые промежуточные переменные, а пути описывают присваивание. Например, на графе для двух переменных X и Y, показанном на рис. 4, путь a  не-XbYc представляет собой присваивание X = 0, Y = 1.

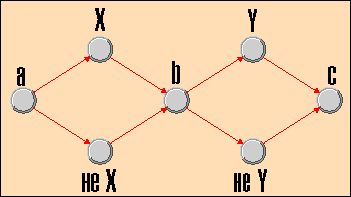
Рис. 4. Граф инициализации для задачи удовлетворения

логического выражения для двух переменных

Вершины и ребра этого графа можно представить отрезками ДНК так же, как это делалось в методе Адельмана. Перемешивание всех этих олигонуклеотидов даст раствор, содержащий ДНК, кодирующие все возможные комбинации входных параметров. Логические операции сводятся к извлечению ДНК, содержащих нужные биты в нужном месте, т. е. к нахождению пути, проходящего через конкретную вершину графа (все как в задаче Гамильтона!).

Рассмотрим, например, случай F = (XY)(XY), и пусть E(t, i, d) - операция извлечения из трубки t всех молекул, где бит i равен d; плюсом обозначим слияние трубок, а присваиванием - переливание их содержимого. Тогда следующая последовательность операций решает поставленную задачу:

t = E(t, 1, 1); t’ = остаток в t

t = E(t’, 2, 1)

t = t+t //остались только молекулы, удовлетворяющие условиям первых скобок

t = E(t, 1, 0); t’ = остаток в t

t = E(t’, 2, 0)

t = t+t //конец. В трубке t - все возможные решения.                     

Взламывание алгоритма шифрования DES

Ни один другой шифр не привлекал к себе так много криптоаналитиков, как американский криптографический стандарт Data Encryption Standard (DES). В принципе эта проблема решаема за приемлемое время и с помощью обычных технологий, но требует концентрации вычислительной мощности десятков тысяч компьютеров. Ученые, занимающиеся исследованием ДНК-машин, просто не могли обойти DES стороной. Массовая параллельность вычислений - как раз то, что требуется для прямой атаки на этот алгоритм.

Сразу несколько групп исследователей предложили свои варианты алгоритмов для нахождения ключа DES по известной паре исходного и зашифрованного текста. Первой оказалась группа Липтона (Dan Boneh, Christopher Dunworth Richard J. Lipton, Breaking DES using a molecular computer. Technical Report CS-TR-489-95, Princeton University, May 1995). Ее подход базировался на утверждении, что DES - это по сути тоже логическая схема.

В частности, исходные данные нужно инициализировать так же, как в общем случае (рис. 5) - рабочая строка алгоритма представляет собой последовательность блоков S, B, S, B, ..., S, где Bi - биты ключа, а Si - служебные последовательности. Далее, используя дополнения к олигонуклеотидам, кодирующим S, и лигазу, в конец этой ДНК можно добавить любые данные. Алгоритм предусматривает хранение в этой области всех промежуточных результатов вычислений. С помощью дополнительных к S “зацепок” можно размножать нужные молекулы методом PCR.

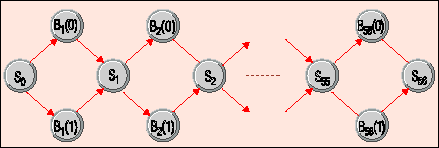
Рис. 5. Граф инициализации ключей для алгоритма шифрования DES

Оригинальным в данном методе является использование природных энзимов для разрезания ДНК (restriction enzimes). Эти белки сканируют ДНК и, если обнаруживают некоторую ключевую последовательность длиной в несколько оснований, режут молекулу пополам. Они используются бактериями для борьбы с вирусами. В данном случае эти энзимы применяются для удаления рабочей информации с конца молекулы.

В целом алгоритм группы Липтона довольно рутинный, и я не стану на нем останавливаться. Большинство предусмотренных им действий сводится к описанной выше операции извлечения данных. В схеме DES, правда, кроме оператора XOR и сдвигов используется еще и поиск по таблицам размера 4x16 элементов, но его легко реализовать с помощью битовой выборки - просто выборок оказывается многовато.

Главное, что задача взламывания DES свелась к следующей: при фиксированном исходном тексте M и полном наборе ключей Ki построить множество из элементов шифрованного текста Ci, таких, где Ci = DES(M, Ki). Так как Ki и Ci будут объединены в итоге на одной ДНК, мы сможем с помощью серии операций побитовой выемки определить по Ci и ключ. Интересно также, что при фиксированном сообщении M раствор с парами (Ki,Ci) достаточно сгенерировать только один раз. Использовать же его можно многократно - подсуньте разок клиенту нужную строку для зашифровки, и все его записи окажутся в ваших руках!

Авторы работы подсчитали, что для достижения результата потребуется осуществить около 900 операций. При современном уровне технологий на это уйдет около 4 месяцев.

Стикеры

Чрезвычайно оригинальная идея была предложена в 1996 г. в работе ряда авторов из Калифорнийского университета и Университета Южной Калифорнии (Sam Roweis et al., A sticker based architecture for DNA computation. см. ftp://hope.caltech.edu/pub/roweis/DIMACS/stickers.ps). Она касается того, как построить ДНК-компьютер, не требующий ни полимеразы, ни лигазы, ни энзимов рестрикции - т. е. “многоразовый”. Более того, в таком компьютере можно будет использовать ДНК-память с произвольным доступом.

Суть идеи очень проста - кодировать нулевые и единичные состояния бита нужно не разными олигонуклеотидами, а присоединением и отсоединением дополнений Ватсона - Крика к ним (рис. 6). Иначе говоря, надо сделать следующее:

1. Задать длину отрезка ДНК, представляющей 1 бит (скажем, M оснований).

2. Если объем памяти в цепочке будет N бит, то построить нужно цепочку олигонуклеотидов длиной N*M оснований, такую, чтобы дополнение к любому ее отрезку длиной M смогло образовать двойную спирать только с этим отрезком (т. е. число несовпадений с любым другим участком было бы велико).

3. Тогда эту цепочку ДНК можно логически разделить на отрезки длиной М и назвать их битами. Если к данному отрезку присоединено его дополнение Ватсона - Крика (так называемый стикер), то бит хранит единицу, в противном случае - ноль. Последовательность олигонуклеотидов, кодирующая отрезок, является адресом в этом блоке памяти.

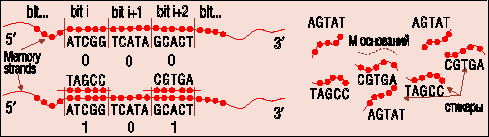
Все операции осуществляются с наборами идентичных ДНК - трубками. С трубками можно делать типовые операции - объединять их, извлекать из них ДНК на основе равенства какого-либо бита нулю или единице. Кроме того, можно добавлять стикеры так, чтобы устанавливать конкретные биты в состояние “1”.

Операция обнуления всего массива осуществляется нагреванием. Отсоединение отдельных стикеров требует более хитрых действий - использования олигонуклеотидов, идентичных стикерам, но имеющих другую опорную структуру (PNA), что придает им способность образовывать с ДНК тройную спираль (!), но в то же время такая спираль оказывается нестабильной и при нагревании разрушается гораздо быстрее, чем двойная, а стало быть, будут удалены только нужные стикеры.

В одном из продолжений своей работы авторы показали, как с помощью этого метода найти ключ алгоритма DES по паре исходный текст - зашифрованный текст.

Вообще говоря, здесь стоит остановиться. В последние годы область быстро развивалась и были предложены методы, как, используя ДНК, моделировать конечные автоматы, осуществлять операции сложения и умножения, перемножать матрицы, вскрывать (по крайней мере теоретически) стойкие шифры типа RC5 и т. п.

Преимущества и недостатки

Напоследок хотелось бы поговорить о перспективах биокомпьютера. Главное преимущество, которое дает ДНК-компьютер, - это беспрецедентная параллельность вычислений. Производительность отдельной ДНК, оценивающаяся в 0,001 операций в секунду, выглядит до безобразия жалкой по сравнению с производительностью обычных ПК, но общая производительность молекул, содержащихся в литре раствора, окажется свыше 10^14 операций в секунду. Самые мощные на сегодня компьютеры имеют скорость порядка 10^12 операций в секунду, но это огромные шкафы с тысячами процессоров, а молекулярный компьютер можно (теоретически) разместить на столе. При этом ДНК-память обеспечит хранение данных с плотностью до 1 бит/нм^3, в то время как современные магнитные ленты работают с плотностями чуть более 10-12 бит/нм^3. Сам же ДНК-компьютер будет способен совершать порядка 2x10^19 необратимых операций на джоуль израсходованной энергии, вплотную приближаясь к теоретическому порогу в 2,4x10^20 оп./Дж, диктуемому соображениями термодинамики. Кремневые системы расходуют на одну операцию в 10^9 раз больше энергии.

Но жизнь не была бы столь сложной, если бы такие красивые идеи легко реализовались на практике. Создать готовый биокомпьютер пока никому не удалось. Было много теоретических построений (типа вскрытия DES), но реально проведено лишь несколько экспериментов, в которых решались относительно простые (с точки зрения современной вычислительной техники) задачи.

Можно выделить несколько проблем, с которыми столкнулись ученые, пытаясь построить биокомпьютер. Основная - это сложность и трудоемкость всех совершаемых операций. По идее, их можно автоматизировать, но это пока сделано лишь частично. Например, остра проблема считывания результата - современные способы секвенсирования далеки от совершенства: скажем, нельзя за один раз секвенсировать цепочки длиной хотя бы в несколько тысяч оснований. Кроме того, это весьма дорогостоящая операция.

Вторая проблема - ошибки в вычислениях. Для биологов точность в 1% при синтезе и секвенсировании оснований считается очень хорошей. Для вычислений же она абсолютно неприемлема. На других этапах - при PCR-усилении, разрезании ДНК энзимами - также не исключено появление ошибок. Решения задачи могут теряться во время операции битовой выемки (молекулы просто прилипают к стенкам сосудов), нет гарантии, что не возникнут точечные мутации в ДНК, и т. д.

Число ошибок экспоненциально растет с числом шагов алгоритма, и весьма возможно, что в конце экспериментатор получит раствор, нисколько не похожий на тот, что должен содержать решение. Проблеме ошибок учеными уделяется большое внимание. Например, Липтон и его коллеги показали, как за счет некоторого увеличения времени работы и объема используемого материала можно изменить вычислительный цикл, чтобы вероятность ошибок была минимальной. Другие группы предлагают использовать не трехмерные, а двумерные ДНК-структуры, где олигонуклеотиды прикрепляются к стеклянной подложке.

Кроме того, биокомпьютер отличается и еще одним неприятным свойством: составляющие его ДНК имеют тенденцию распадаться с течением времени. Иначе говоря, результаты вычислений тают на глазах! Для борьбы с этим явлением некоторые авторы предлагают использовать специальные белковые взвеси, в которые и помещать ДНК.

Также в некоторых работах оспаривается сама возможность масштабирования всей системы уровня, пригодного для решения действительно сложных задач.

Все эти примеры показывают, насколько биокомпьютер пока далек от понятия “практически полезная вещь”. Стремительное развитие технологий может существенно изменить ситуацию, но насколько верен базовый подход? Сейчас он состоит в моделировании алгоритмов на макроуровне такими операциями, как сливание и разливание сосудов. Но более перспективным было бы создавать наномашины, похожие на природные энзимы, но формирующие результат по другим законам. Скажем (фантазируя по максимуму), можно вообразить энзим, который на базе существующей ДНК, содержащей ключ DES, синтезирует другую, но уже шифрующую сообщение. Это безумно сложно (что касается DES, то вряд ли вообще возможно), но это то, к чему рано или поздно придет нанотехнология. Вполне вероятно, что от макроопераций не удастся избавиться навсегда, но их число будет многократно уменьшено.

В общем, станет ли биокомпьютер реальностью или не выдержит конкуренции с другими нарождающимися технологиями (например, квантовыми вычислениями), пока неясно. Но сама идея очень красива, как и все то, что придумала природа безо всякого нашего участия и что достойно искреннего восхищения!

Если вас заинтересовала тема, пишите мне по адресу: vladik@pcweek.ru.

P.S. Чтобы не загромождать статью, я не стал давать подробные ссылки на статьи непосредственно в тексте. В принципе, исчерпывающую библиографию можно найти в Интернете по адресам: http://www.geocities.com/ResearchTriang … naftp.html и http://design.alfred.edu/DNAcomputing. Прочитать о белках, ДНК и т. п. можно в труде Департамента энергетики США Primer on Molecular Genetics (http://www.ornl.gov/hgmis/publicat/primer/intro.html).

Даже если бы лазер работал так как ты себе представляешь, то это ничего не изменило бы. Сам подход лишен смысла.

И как узел, получивший сигнал, будет узнавать в какой узел ему дальше передавать модифицированный сигнал?

Откуда?

И что с того? Про него известно только то, что он прошел все узлы, а в каком порядке - неизвестно. В том числе нет информации по точкам входа и выхода.
Даже если произошло чудо и после отбраковки всех запрещенных остался один правильный вариант, то мы про этот маршрут все равно ничего не знаем, а тупо имеем перечень всех узлов. Который мы и так знаем исходно.
Проблема в этом, а не в лазырях и технической реализации.

Лукомор
Издеваешься что-и? Я топик про коммивояжера с этого начал.
Первый разрешенный кратчайший даст время и точку выхода. Дальше бинарным поиском от последней к первой. Выше же написано

это же элементарно
дифракционная решетка
плюс интерференция и проэцирование на идеальную прямую сбоку

Знаем. Потому что ниже

Время даст исключительно в какой-то точке

С чего это они будут накладываться, если у все у них различное время прихода в точку? Разнести их по времени - дело техники

Зачем??? Во первых это отдельные вспышки. Во вторых их будет много меньше, чем (N-1)!, поскольку останов будет по получению первого же разрешенного

значит
при одном входе
ВЫХОДА НЕТ ????