Лом в качестве сертифицированного генератора случайных чисел, очень даже!

Не случайного, а произвольного

Мы привыкли, что наука может предсказывать, но вот такие вещи принципиально неприводимы [к более простому уровню]. Единственный способ узнать результат процесса – это, по сути, наблюдать за его развитием
(с) С.Вольфрам
До Вольфрама считалось, что математика всемогуща и всегда можно найти короткий способ получения результата - формулу изрбрести.

Штука в том, что это оказалось принципиально невозможным

Там в общем случае именно в этом и проблема. Метрологи в принципе не могут измерять начальные условия, так чтобы задача стала решаема. И не потому, что это метрологи такие, а потому что задача имеет неустойчивое решение. Таких задач море. Это такой же закон природы, который труден для осознания, как и второе начало термодинамики. Заточеный карандаш, установленный на острие все равно упадет и мы все равно не сможем сказать в какую сторону, шарик катящийся по лезвию ножа все равно упадет, но мы не сможем решить, в какую сторону он упадет, машинка Зенера все равно провернется, но мы не сможем предсказать, в каком направлении и т. п.

Если вычислитель сильнее задачи то приводимая куда угодно. А если задача сильнее, то неприводимая никуда кроме того места, куда сама задача стремится.

Я даже представить это боюсь! Опять же классика -

Вы с Вольфрамом уже не в первый раз несёте пургу.
Объясняю для обоих. Вывести формулу - исключительный удел алгебры. Но в математике есть очень много чего, кроме алгебры.
Никто не мешает просчитать каждый эволюционный шаг автомата и получить его состояние на любом шаге эволюции. Исключительно математическими методами и не выходя за рамки математики.
Так что математика может считать эволюцию клеточных автоматов, для этого не существует никаких проблем.

Не знаю кто это придумал. Большое количество практических задач не имеют алгебраического решения. Я бы даже сказал, что подавляющее. Ответ все равно находят, численно, моделированием, пошаговым решением, разбиением на части, приближениями. Люди умнее математики.

Вот! Золотые слова!
Как достойный представитель когорты самых умных людей в отставке,
целиком и полностью одобряю процитированное замечание.

Тут такое дело...
Сегодня она неприводимая, а завтра, глядишь, и привелась!

Вот простой арифметический пример:

Числа Фибоначчи, весьма характерный пример алгебраически неприводимой задачи.
То-есть зздав всего лишь первые два  элемента последовательности, например,
p(0)=1 и p(1)=1
и простое правило индукции:
p(n)=p(n-1)+p(n-2), можем последовательно, пошагово,
найти сколько угодно элементов этой последовательности, например так:
p(2)=p(1)+p(0)=1+1=2
p(3)=p(2)+p(1)=2+1=3
p(4)=p(3)+p(2)=3+2=5
И.т.д...
Но никакими алгебраическими преобразованиями нельзя вывести формулу,
по которой можно сразу, не проходя всех этих последовательных шагов,
подставить в эту формулу, например n=9, и получить p(9)=55.
Это и будет алгебраически неприводимая задача.
Но хочется ведь сразу!
И тут на помощь приходит матанализ, теория дифференциальных уравнений и
мсчмсление конечных разностей.
Прстенькое дифуравнение: y"=y'+y c начальными условиями:
y(0)=1. и y(1)=1, дает нам сразу решение: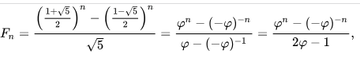
,
где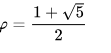

- "золотое сечение".
Подставив в эту формулу любое n получим сразу энное
число Фибоначчи.
При этом последовательность останется алгебраически неприводимой,
в то же время являясь уже аналитически приводимой.

Отредактировано Лукомор (2023-06-02 16:31:27)

Поскольку комбинаторика на деле предваряет теорию вероятности, заключаем,
что комбинаторика и есть теория информации!

Так Шарпер с Вольфрамом.

При этом вероятность того, что все пассажиры в самолете - блондинки, довольно низкая, если их все перемножить, то вообще ноль. Тем не менее, если уж такой самолет все-таки соберется, то вероятность, что он встретит в полете динозавра, всё равно 1/2.

В значительном количестве практических задач даже при такой приводимости численный алгоритм все равно более ресурсосберегающий.

*пересчитывает пальцы* Не. Я, даже когда падал с лестницы с работающей болгаркой запутавшейся в намордной повязке преьбывал в меланхолии.

Ну так да! Заметь, что и с кубиком то же самое. Это у кубика шесть вариантов, а у игрока только два - выигрыш и проигрыш.

Правильно, но потому что у самолета, как у кубика, вариантов больше