Топик для комментариев и кратких обсуждений из "Ленты новостей". Убедительная просьба для полновесных дискуссий заводить отдельные топики.
Обсуждение - Физика
Сообщений 1681 страница 1710 из 1711
Поделиться12015-03-03 22:25:37
- Ветеран
- Уважение: +654
- Провел на форуме:
1 месяц 4 дня - Последний визит:
2018-04-05 22:45:12
Поделиться16812025-03-17 06:58:45
- Ветеран
- Уважение: +7634
- Пол: Мужской
- Провел на форуме:
3 месяца 18 дней - Последний визит:
Сегодня 09:39:49
#p199022,Шарпер написал(а):
Щас еще один чертеж найду
Если говорить "А если еще один чертеж найду?", то это будет производить на собеседника более устрашающее действие.
Поделиться16822025-03-17 07:33:45
- Дичинка
- Уважение: +1416
- Пол: Мужской
- Провел на форуме:
6 месяцев 1 день - Последний визит:
Сегодня 07:50:30
#p199019,Лукомор написал(а):
А какая нам разница, если это одно и то же колесо, и оно вокруг оси вращается.
Устремим r к нулю.
Не нажо умтремлятть ось к нулю!!!
Если на оси, то без разницы, ты просто отнимешь хлеб у "физиков-парадоксников"прогулявших теормех и ничего не знающих о ТММ. На оси считают обороты а не развертки. А тут именно развертки и их соотношение как ведущей и ведомой. Катишь по маленькому, смотришь сколько не докатилось ведомое большое, по большому, смотришь сколько перекатило малое.
Поделиться16832025-03-17 07:36:14
- Дичинка
- Уважение: +1416
- Пол: Мужской
- Провел на форуме:
6 месяцев 1 день - Последний визит:
Сегодня 07:50:30
#p199023,Zagar написал(а):
Если говорить "А если еще один чертеж найду?", то это будет производить на собеседника более устрашающее действие.
Я предложил провести опыт с пирамидкой
Поделиться16842025-03-17 08:15:48
- Модератор
- Уважение: +14655
- Провел на форуме:
7 месяцев 16 дней - Последний визит:
Сегодня 10:17:25
Пирамидок должно быть пять. Четыре по углам и одна в центре комнаты. Это я как специалист говорю.
Поделиться16852025-03-17 08:56:08
- Дичинка
- Уважение: +1416
- Пол: Мужской
- Провел на форуме:
6 месяцев 1 день - Последний визит:
Сегодня 07:50:30
#p199026,DoctorLector написал(а):
Пирамидок должно быть пять. Четыре по углам и одна в центре комнаты. Это я как специалист говорю.
Ну, можно на обрезок карандаша изоленту навертеть
Поделиться16862025-03-17 14:04:30
- Модератор
- Уважение: +14655
- Провел на форуме:
7 месяцев 16 дней - Последний визит:
Сегодня 10:17:25
#p199027,Шарпер написал(а):
можно на обрезок карандаша изоленту навертеть
Какое-то антисемитское изделие получится.
Поделиться16872025-03-17 15:01:20
- Дичинка
- Уважение: +1416
- Пол: Мужской
- Провел на форуме:
6 месяцев 1 день - Последний визит:
Сегодня 07:50:30
#p199029,DoctorLector написал(а):
Какое-то антисемитское изделие получится.
Чо? 
Поделиться16882025-03-17 15:44:05
- Ветеран
- Уважение: +5855
- Провел на форуме:
6 месяцев 6 дней - Последний визит:
2025-03-26 19:54:31
#p199024,Шарпер написал(а):
Катишь по маленькому, смотришь сколько не докатилось ведомое большое, по большому, смотришь сколько перекатило малое.
А теперь попробуй катить по маленькому и по большому одновременно...
Поделиться16892025-03-17 15:52:50
- Модератор
- Уважение: +14655
- Провел на форуме:
7 месяцев 16 дней - Последний визит:
Сегодня 10:17:25
#p199034,Лукомор написал(а):
попробуй катить по маленькому и по большому одновременно
*с профессиональным интересом*
И что, помогают ему советы?
Поделиться16902025-03-17 16:01:10
- Дичинка
- Уважение: +1416
- Пол: Мужской
- Провел на форуме:
6 месяцев 1 день - Последний визит:
Сегодня 07:50:30
#p199034,Лукомор написал(а):
А теперь попробуй катить по маленькому и по большому одновременно...
С какой целью? Какой диаметр, а точнее длина его развертки будет управляющей?
Поделиться16912025-03-17 16:09:10
- Ветеран
- Уважение: +5855
- Провел на форуме:
6 месяцев 6 дней - Последний визит:
2025-03-26 19:54:31
#p199037,Шарпер написал(а):
Какой диаметр, а точнее длина его развертки будет управляющей?
Обе, естественно, будут управляющими.
Поделиться16922025-03-17 16:15:28
- Ветеран
- Уважение: +5855
- Провел на форуме:
6 месяцев 6 дней - Последний визит:
2025-03-26 19:54:31
#p199035,DoctorLector написал(а):
И что, помогают ему советы?
Нет... И даже немножечко вредят...
Поделиться16932025-03-17 16:17:37
- Дичинка
- Уважение: +1416
- Пол: Мужской
- Провел на форуме:
6 месяцев 1 день - Последний визит:
Сегодня 07:50:30
#p199038,Лукомор написал(а):
Обе, естественно, будут управляющими.
Не будут, будет "ПРОСКЛИЗЫВАНИЕ" по галилеевски с привязкой к большой развертке.
Еще раз., кати малое колесо на оборот, убедись сам
Поделиться16942025-03-17 16:28:50
- Ветеран
- Уважение: +5855
- Провел на форуме:
6 месяцев 6 дней - Последний визит:
2025-03-26 19:54:31
#p199040,Шарпер написал(а):
будет "ПРОСКЛИЗЫВАНИЕ" по галилеевски с привязкой к большой развертке.
Почему именно к большой?
Поделиться16952025-03-17 16:30:13
- Дичинка
- Уважение: +1416
- Пол: Мужской
- Провел на форуме:
6 месяцев 1 день - Последний визит:
Сегодня 07:50:30
#p199038,Лукомор написал(а):
Обе, естественно, будут управляющими.
Что-то я начинаю подозревать, что ты сам не понимаешь что хочешь доказать.
Мой тезис - парадокса нет, он был у Аристотеля по неразвитости теормеха
Ращвертка зависит от радиуса, как и циклоида.
Теперь озвучь свои
Поделиться16962025-03-17 16:30:46
- Ветеран
- Уважение: +5855
- Провел на форуме:
6 месяцев 6 дней - Последний визит:
2025-03-26 19:54:31
#p199040,Шарпер написал(а):
Еще раз., кати малое колесо на оборот, убедись сам
Убедиться в чем именно?
Поделиться16972025-03-17 16:32:21
- Дичинка
- Уважение: +1416
- Пол: Мужской
- Провел на форуме:
6 месяцев 1 день - Последний визит:
Сегодня 07:50:30
#p199041,Лукомор написал(а):
Почему именно к большой?
А иначе оборот будет неполным, а по малому D
Поделиться16982025-03-17 16:36:32
- Дичинка
- Уважение: +1416
- Пол: Мужской
- Провел на форуме:
6 месяцев 1 день - Последний визит:
Сегодня 07:50:30
#p199043,Лукомор написал(а):
Убедиться в чем именно?
В неполном обороте большого D. Маленькая развертка меньше, чем нужно для полного оборота D
Поделиться16992025-03-17 16:42:49
- Ветеран
- Уважение: +5855
- Провел на форуме:
6 месяцев 6 дней - Последний визит:
2025-03-26 19:54:31
#p199042,Шарпер написал(а):
ты сам не понимаешь что хочешь доказать.
Я, собственно, ничего не хочу доказать...
Я здесь иллюстрирую известный афоризм неизвестного автора:
"Сложные задачи имеют простые и легкие для понимания неправильные решения!"
Поделиться17002025-03-17 16:52:22
- Ветеран
- Уважение: +5855
- Провел на форуме:
6 месяцев 6 дней - Последний визит:
2025-03-26 19:54:31
#p199044,Шарпер написал(а):
А иначе оборот будет неполным, а по малому D
Оборот будет 360 градусов, хоть по r=0
Они же жестко на одной оси...
Поделиться17012025-03-17 16:55:55
- Дичинка
- Уважение: +1416
- Пол: Мужской
- Провел на форуме:
6 месяцев 1 день - Последний визит:
Сегодня 07:50:30
#p199046,Лукомор написал(а):
Я, собственно, ничего не хочу доказать...
Я здесь иллюстрирую известный афоризм неизвестного автора:
"Сложные задачи имеют простые и легкие для понимания неправильные решения!"
Т.е. ты не понимаешь что "парадокс" порожден бредовым вопросом и при этом не желаешь сделать простейший опровергающий опыт?
Поделиться17022025-03-17 16:59:25
- Дичинка
- Уважение: +1416
- Пол: Мужской
- Провел на форуме:
6 месяцев 1 день - Последний визит:
Сегодня 07:50:30
#p199047,Лукомор написал(а):
Оборот будет 360 градусов, хоть по r=0
Они же жестко на одной оси...
да. Но только оборот малого даст короткую развертку и остсновит большой на неполном обороте
r=0 быть тут не может. Это не колесо
Отредактировано Шарпер (2025-03-17 17:05:07)
Поделиться17032025-03-17 17:14:41
- Ветеран
- Уважение: +5855
- Провел на форуме:
6 месяцев 6 дней - Последний визит:
2025-03-26 19:54:31
#p199045,Шарпер написал(а):
В неполном обороте большого D. Маленькая развертка меньше, чем нужно для полного оборота D
Для полного оборота большого D не нужно ничего, кроме полного оборота большого D.
Вот иллюстрация вращения большого D вокруг маленького d, который суть точка в центре большого D - его ось вращения по гамбургскому счету.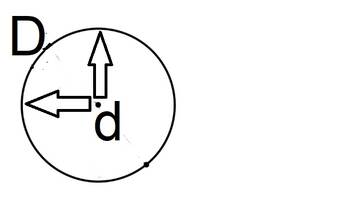
Маленькая развертка в этом случае равна нулю, но этого достаточно, чтобы D совершил полный оборот, за то же время, за которое d совершает один полный оборот...
Поделиться17042025-03-17 17:26:49
- Ветеран
- Уважение: +5855
- Провел на форуме:
6 месяцев 6 дней - Последний визит:
2025-03-26 19:54:31
#p199048,Шарпер написал(а):
ты не понимаешь что "парадокс" порожден бредовым вопросом
Каким вопросом?
Поделиться17052025-03-17 17:29:34
- Дичинка
- Уважение: +1416
- Пол: Мужской
- Провел на форуме:
6 месяцев 1 день - Последний визит:
Сегодня 07:50:30
Аоисттотеля - почему колеса ведут себя как равного диаметра
Отредактировано Шарпер (2025-03-17 17:32:08)
Поделиться17062025-03-17 17:29:58
- Ветеран
- Уважение: +5855
- Провел на форуме:
6 месяцев 6 дней - Последний визит:
2025-03-26 19:54:31
#p199048,Шарпер написал(а):
при этом не желаешь сделать простейший опровергающий опыт?
Какой опыт?
У парадоксов обычно не бывает опровергающих опытов.
"Парадокс - это не ошибка, парадокс - это... парадокс!"(с) Лукомор
Поделиться17072025-03-17 17:32:17
- Ветеран
- Уважение: +5855
- Провел на форуме:
6 месяцев 6 дней - Последний визит:
2025-03-26 19:54:31
#p199049,Шарпер написал(а):
Это не колесо
Круглое, как колесо, катится, как колесо, и не колесо?
Чур меня!
Поделиться17082025-03-17 17:33:48
- Дичинка
- Уважение: +1416
- Пол: Мужской
- Провел на форуме:
6 месяцев 1 день - Последний визит:
Сегодня 07:50:30
#p199053,Лукомор написал(а):
Какой опыт?
У парадоксов обычно не бывает опровергающих опытов.
"Парадокс - это не ошибка, парадокс - это... парадокс!"(с) Лукомор
Это не парадокс, а неразвитость теормеха во времена Аристотеля
Поделиться17092025-03-17 17:35:23
- Дичинка
- Уважение: +1416
- Пол: Мужской
- Провел на форуме:
6 месяцев 1 день - Последний визит:
Сегодня 07:50:30
#p199054,Лукомор написал(а):
Круглое, как колесо, катится, как колесо, и не колесо?
Чур меня!
Ну покати колесо r=0 , если найдешь
Поделиться17102025-03-17 17:55:39
- Модератор
- Уважение: +14655
- Провел на форуме:
7 месяцев 16 дней - Последний визит:
Сегодня 10:17:25
#p199053,Лукомор написал(а):
У парадоксов обычно не бывает опровергающих опытов.
Как сказал бы Петька в анекдоте: "Какие ещё парадоксы? Я с тобой после нюансов не разговариваю".
